Overview On Java Data Structures
Java comes with a wide variety of standard data structures. While they are all to some extent "alike" (they all store objects in one way or another), each serves a specific purpose.
| Data Structure | Image | What Is This? | Typical Operations (Pseudocode) | Typically Use For ... |
|---|---|---|---|---|
| Array | 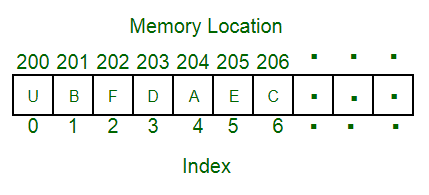 Fullsize Image / Reference |
Static data structure, referenced via indices | intArray[i][j] = ... |
Fixed amount of data (cannot grow), easy access, mathematical operations |
| List | 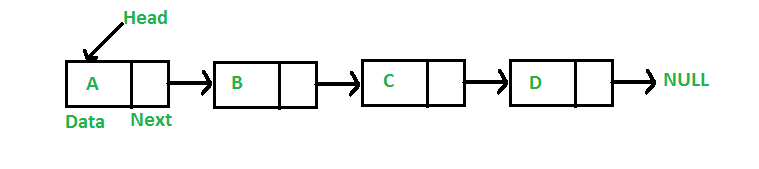 Fullsize Image / Reference |
Objects connected by (usually) bidirectional links | list.add(i, obj) list.get(i) list.iterator() |
Dynamic, linear structures, where objects can be added at start, end, or middle |
| Stack | 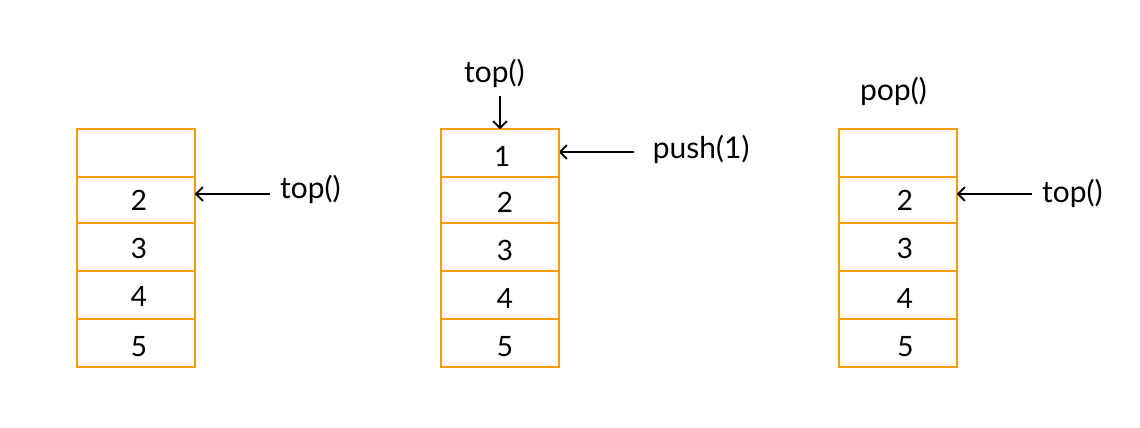 Fullsize Image / Reference |
List where objects can only added and removed on top | stack.top() stack.push(obj) stack.pop() |
Task management using LIFO (last in, first out) principle |
| Queue |  Fullsize Image / Reference |
List where objects added on one end, and taken out at the other | queue.enqueue(obj) queue.dequeue() |
Manage tasks according to waiting line (FIFO, first in, first out) principle |
| Map |  Fullsize Image / Reference |
Implements a function key => value (object) \ |
map.set(i, obj) map.get(i) |
Manage a limited number of objects with a huge range of possible keys, with quick access |
| Set |  Fullsize Image / Reference |
Contains an object at max once | set.add(obj) set.remove(obj) set.contains(obj) |
Manage structures where duplicates need to be removed |
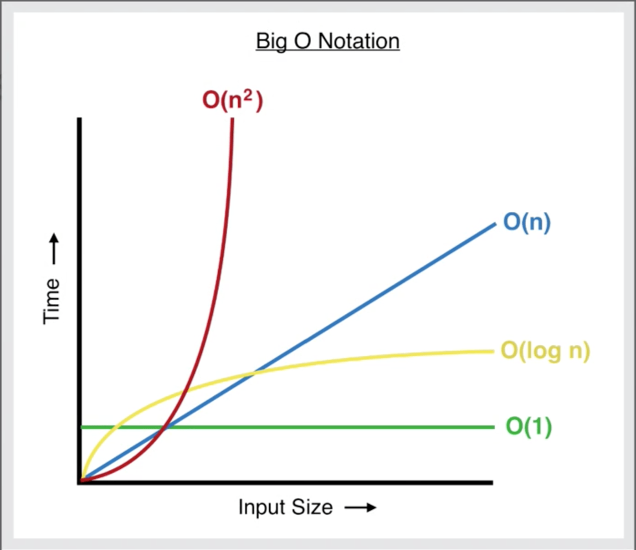
Big-O Notation
The big-O notation "O(...)" is a way of expressing how well a data structure performs with growing numbers of elements.
- O(1): Effort is (more or less) constant, regardless of the number of elements. Great for large number of elements. May be slow (in absolute time), though. So, suitability for small number of elements need to be checked in each case.
- O(log(n)): 2nd-best option for large numbers - the larger the number, the closer to constant effort.
- O(n): suited for small numbers, less so for large numbers.
- O(n2) (and all higher potences or exponential orders ...): avoid for large numbers!
Effort For Typical Operations In The Various Data Structures
Assumption in the following table: The element that is inserted / accessed / searched for / deleted is located "somewhere in the middle" of the structure.
| Data Structure | Insert | Access | Search | Delete | Comments |
|---|---|---|---|---|---|
| Array | O(n) | O(1) | O(log(n)) | O(n) | Assumption for search effort: binary search (interval splitting), linear search is O(n) |
| List | O(n) | O(n) | O(n) | O(n) | |
| Stack | O(1) | O(1) | - | O(1) | insert / access / delete refers to the top-most element only, search is not supported |
| Queue | O(1) | O(1) | - | O(1) | insert refers leftmost element only, access / delete to rightmost only, search is not supported |
| HashMap | O(1) | O(1) | O(1) | O(1) | Implemented using hash array |
| TreeMap | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | Implemented using binary search tree |
| Set | O(1) | O(1) | O(1) | O(1) | Assumption: Implemented using HashMap |