Algorithms
Graphs
Graphs play a critical role in computer science. Here is an example of an undirected graph:
There are two main ways to represent a graph.
Adjacancy Matrix
Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.
Adjacancy List In The Vertices (Nodes)
An array of lists is used. Size of the array is equal to the number of vertices. Let the array be array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is adjacency list representation of the above graph.
(Examples and explanations taken from https://www.geeksforgeeks.org/graph-and-its-representations/)
Graph Exercise
Take the following graph showing cities and their distances.
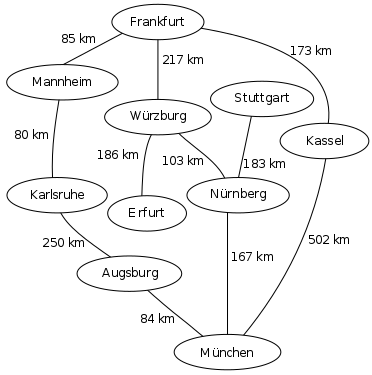(Example taken from https://de.wikipedia.org/wiki/Dijkstra-Algorithmus)
- Choose the most appropriate representation for this graph.
- Implement the graph.
- Write a method that outputs the graph to console, in the way as described below.
Frankfurt
Mannheim: 85 km
Würzburg: 217 km
Kassel: 173 km
Mannheim
Karlsruhe: 80 km
Frankfurt: 85 km
...
Dijkstra Algorithm
The Dijkstra algorithm is an algorithm that allows finding the shortest path between two graph nodes. Please implement the Dijkstra algorithm on the graph shown above.
You find a good description (pseudocode + visual explanation) in the Wikipedia article on it: https://de.wikipedia.org/wiki/Dijkstra-Algorithmus.